 |
 |
 |
 |
 |
 |
My research focuses on systems of metamorphic robots. These systems, a subset of self-reconfigurable robot systems, are collections of independent, mobile robots (modules) that have the ability to change shape through the connection, disconnection and rotation of individual modules. Metamorphic robots have the property of being uniform in structure and capability, and typically possess regular symmetry so that they can be closely packed with few gaps between them. The movement of modules within metamorphic robot systems is dependent on hardware, however locomotion is generally achieved by modules "crawling" across a substrate composed of adjacent robots.
The ability of metamorphic robots to alter their shape suggests their usefulness in environments not amenable to direct human observation, such as deep space or ocean floors. These systems are also envisioned for use in tasks such as building temporary bridges, forming buttresses, and excising tumors.
My specific work with metamorphic robots concentrates on systems
composed of any number of two-dimensional, hexagonal modules.
Modules each occupy a single cell in the plane and are aware at all
times of their location both in the plane and relative to their neighbours.
Movement occurs in lockstep rounds and reconfiguration relies on finding a
contiguous path of cells (a substrate path) that spans the goal, on which
robots may crawl without collision or deadlock.
Summer Work
During the summer of 2002, my mentors and I worked to develop
algorithms for reconfiguration when a single obstacle was present in
the goal environment (an "enveloped" obstacle). We defined
admissibilty conditions for obstacles by extending the notion of
an admissible substrate path to create the concept of an
admissible surface. We also developed strategies to "repair" an
obstacle's surface to ensure that modules did not become trapped when
climbing across it.
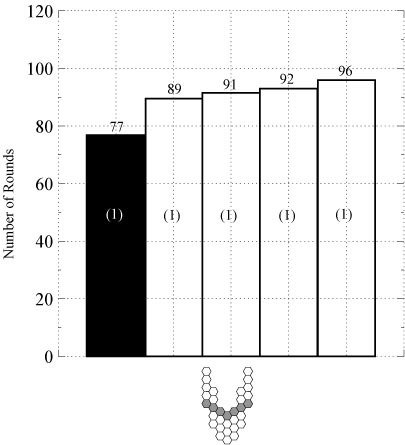
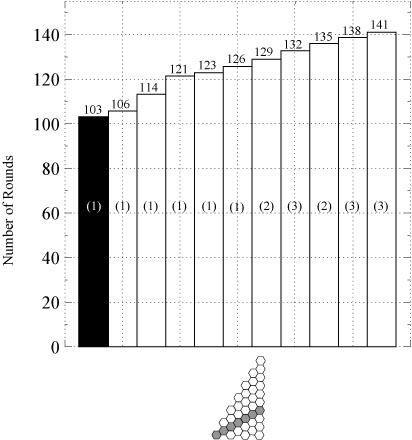
We also ran several simulations to test the effectiveness of our graph traversal algorithm (presented in our ICRA 2002 paper, see below) at choosing the "fastest" path for reconfiguration in terms of the number of rounds. The graphs, below, show the results of some of these simulations for two goal shapes. Each bar indicates the number of rounds needed to fill in the goal using a particular substrate path. The shaded bar represents the substrate path chosen by our algorithm as being the fastest. The numbers in parenthesis inside each bar indicates the number of executions that used that number of rounds.
 |
 |
We likewise conducted simulations to determine the efficiency of the graph traversal algorithm. To this end, we ran the algorithm on a number of different goal shapes and counted the number of vertex visits performed by the algorith. The results are presented in the table, below, where n is the number of modules in the system, c is the number of columns in the goal shape, and r is the number of rows.
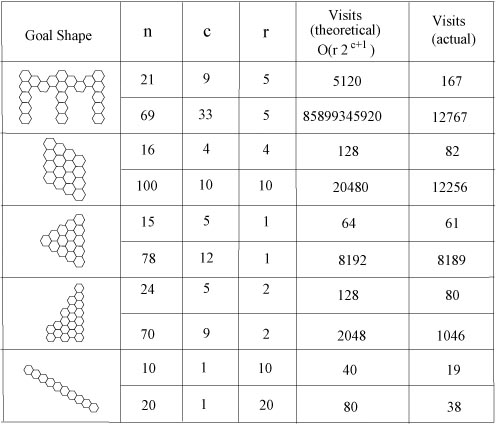
The results of these simulations, as well as our strategies for coping with enveloped obstacles during reconfiguration, will be discussed in full in our upcoming journal paper. Our most recent work can be found in our ICRA 2003 paper, available here. Our ICRA 2002 work is also available.
Walter, J. E. Tsai and N. Amato. Enveloping obstacles with hexagonal metamorphic robots. To appear, Proc. of IEEE Int'l. Conf. on Robotics and Automation, May 2003.
Walter, J., E. Tsai and N. Amato. Choosing good paths for fast distributed reconfiguration of hexagonal metamorphic robots. In Proc. of IEEE Int'l. Conf. on Robotics and Automation, 2002.