Simultaneous Q-learning: No Pricebot has a Fixed Action

The main reason to look at the Q tables resulting from one pricebot fixing its action is as a check that things are working correctly. What we are really interested in though, is what the Q tables look like when neither pricebot always chooses a fixed action. Hence, this section presents the Q tables for simultaneous update when neither pricebot plays a fixed action. Our simultaneous results presented in this section do not quite match what they should be. The Q tables should converge to the payoff table when $\gamma$ equals zero, since the payoffs are being used as the reward, and if $\gamma$ is greater than zero then the Q table should look like the payoff table except now with $\gamma$ taken into account [3]; however that is not what happened. What we found was the following. Since we calculated what the Q tables should look like as well as determined the Q tables experimentally and got similar results, there is an error in the calculations we did. However, the calculations done and the results found are presented here although it is recognized that there are errors.

Table 7 presents the calculated Q values for simultaneous update. The Q values in Table 7 were calculated in the following way. First we calculated the averages of each column of the payoff matrix in Table 3, see Table 6.

Column	Average
0.5	0
0.6	0.06875
0.7	0.1125
0.8	0.13125
0.9	0.125
1.0	0.09375

Table 6. Averages of columns in the payoff matrix.

Next, we know that action 0.7 is being played with probability 1-$\epsilon$ and other actions are being played with probability $\epsilon$. We are using an $\epsilon$ of 0.05. We used the equation below to calculate each entry in Table 7 using this information. For state x and action y:

$Entry_{xy} = Payoff_{0.7y}\cdot(1-\epsilon) + Average_y \cdot \epsilon$

where payoff_0.7y is the payoff for action y when in state 0.7 and average_y is the average of the entries for column y.

state/action	0.5	0.6	0.7	0.8	0.9	1.0
0.5	0	0.0865625	0.100625	0.0421875	0.05375	0.0640625
0.6	0	0.0865625	0.100625	0.0421875	0.05375	0.0640625
0.7	0	0.0865625	0.100625	0.0421875	0.05375	0.0640625
0.8	0	0.0865625	0.100625	0.0421875	0.05375	0.0640625
0.9	0	0.0865625	0.100625	0.0421875	0.05375	0.0640625
1.0	0	0.0865625	0.100625	0.0421875	0.05375	0.0640625

Table 7. Calculated Q table for wA=0.25, wB=0.75 and simultaneous update. Does not take 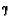$\gamma$ into account. These are the Q values the QL Q tables should converge to.

The reason why all the entries are the same in each column in Table 6A and 6B is that we are adding the same payoff value from the 0.7 state to the same average column value. We can now look at the experimental results for when neither QL pricebot is playing a fixed action. The experimental results that we get, see Table 9, are very similar to the calculated Q tables in Table 7. Interestingly, we see that Q values for the actions for each state end up looking like the Q values for the actions for state 0.7. For the simultaneous learning, after 500 million rounds with the 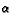$\alpha$-decay-like decaying $\epsilon$ we get Table 8.

state/action	0.5	0.6	0.7	0.8	0.9	1.0
0.5	0.0001012	0.0857952	0.101123	0.0464701	0.056763	0.0647148
0.6	0.000101193	0.0859425	0.102011	0.0465411	0.0576224	0.0655664
0.7	0.000101254	0.0859014	0.100776	0.0471251	0.0571762	0.0655254
0.8	0.000101306	0.0859675	0.101669	0.0463068	0.0564989	0.0647921
0.9	0.000101317	0.0859112	0.101598	0.0453765	0.0570052	0.0652384
1.0	0.000101296	0.0862614	0.101436	0.0469018	0.0562795	0.0658477

Table 8. After 499999999 rounds. Is in state 2 and action 2 on this round (2 = 0.7, 2 = 0.7). Simultaneous, wA=0.25, wB=0.75, pricebots choose a random action for a state with probability of $\epsilon$ and choose the best action with probability 1-$\epsilon$. $\epsilon$ is decaying and when this table was made, $\epsilon$ had decayed to 0.09091. The old Q value - the new Q value is 6.14722e-07.

If we make a graph of the best responses for each state for each player, based on the Q tables, we get the graph in Figure 2. The Q tables we used are Tables 8A and 8B. These were the two tables available that there was data from each player so they were used. Although they do use the pseudo-$\epsilon$ decay, it is irrelevant, and with time, tables that use the regular $\epsilon$ decay could be made and another graph, and this graph would be identical to the graph in Figure 2 The pseudo $\epsilon$ decay used is below and it was kind of a hack to try and eventually get a small $\epsilon$. 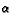Looking at the $\epsilon$ decay function (like the $\alpha$ decay) in gnuplot, but it seemed that if $\epsilon$ could be made to decay to a very small number after 100 million rounds, then it would not have spent sufficient time randomly exploring.

The pseudo-$\epsilon$ decay is,

if	(currRound > 90000000)
	$\epsilon_n = 0.0001;$
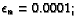else if	(currRound > 50000000)
	$\epsilon_n = 0.001;$
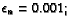else if	(currRound > 10000000)
	$\epsilon_n = 0.01;$
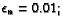else if	(currRound > 1000000)
	$\epsilon_n = 0.05;$
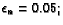else if	(currRound > 500000)
	$\epsilon_n = 0.50;$
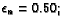else
	$\epsilon_n = 1.0;$

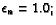A. state/action	0.5	0.6	0.7	0.8	0.9	1.0
0.5	0.00010024	0.0868088	0.100121	0.0405321	0.053697	0.0633732
0.6	0.000100298	0.0869526	0.100055	0.0420465	0.0547109	0.06311
0.7	0.00010011	0.0876	0.1001	0.0376307	0.0502007	0.0626128
0.8	0.000101017	0.0867011	0.100106	0.042365	0.0534665	0.0639472
0.9	0.000101066	0.0863434	0.100093	0.0440427	0.0542756	0.0637399
1.0	0.000100977	0.0870105	0.100091	0.0432934	0.0522114	0.0639043
B. state/action	0.5	0.6	0.7	0.8	0.9	1.0
0.5	0.000100323	0.0869103	0.100102	0.0447314	0.0540285	0.0636493
0.6	0.000100411	0.0862549	0.10007	0.0435341	0.0545976	0.0632749
0.7	0.000100111	0.087599	0.1001	0.0376873	0.0503039	0.062612
0.8	0.000101007	0.0865916	0.100086	0.0401568	0.0516071	0.0646759
0.9	0.000101004	0.086484	0.100055	0.0421205	0.0563015	0.0650803
1.0	0.000100988	0.0867745	0.100099	0.0409425	0.0573791	0.0643089

Table 9. After 99999999 rounds for both pricebots. Both pricebots are in state 0.7 and action 0.7 on this round. Simultaneous update with wA=0.25 and wB=0.75. 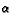$\alpha$is decaying starting at 0.01. Note that 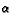$\alpha$is not fixed. $\epsilon$ has decayed to 0.0001 using the pseudo-$\epsilon$ decay at this point. Pricebots choose a random action for a state with probability of $\epsilon$ and choose the best action with probability 1-$\epsilon$ A. 1st qpricebot's table. The old Q value - the new Q value is 0. B. 2nd qlpricebot's table. The old Q value - the new Q value is 2.07917e-13.

Figure 2. Simultaneous, made from Tables 8A and 8B. The arrow indicates the Nash equilibrium of 0.7, 0.7.

We now have a possible explanation for why the Q values for the actions for each state end up looking like the Q values for the actions for state 0.7: from Figure 2 we see that 0.7, 0.7 is the Nash equilibrium. However this does not explain why the Q values choose to end up at the Nash equilibrium instead of converging to the payoff matrix. Basically, the Q values should be converging to the payoff matrix and they are not. Since the sequential qlearning seems to be working correctly, there is probably an error in the order the updating is done for the simultaneous qlearning algorithm rather than the qlearning algorithm itself.

When the min price (the other pricebot's price) from the previous round is used as the state for simultaneous, the Q tables converge to all state 7 payoffs as we just saw in Table 9. When the current min price is used as the state, one Q table converges to all state 7 payoffs, the other Q table for the other player converges to the payoff table. See Table 10.

A. state/action	0.5	0.6	0.7	0.8	0.9	1.0
0.5	0.000106471	0.0783584	0.106332	0.0843278	0.0871126	0.0776166
0.6	0.000106473	0.0779367	0.106332	0.0843748	0.0878633	0.0785019
0.7	0.000106442	0.0779623	0.106326	0.0842921	0.0865126	0.0786863
0.8	0.000106468	0.078454	0.106564	0.0840732	0.0880429	0.0781503
0.9	0.000106473	0.0783395	0.106283	0.0844303	0.0883922	0.0782733
1.0	0.000106463	0.0784538	0.106266	0.0854391	0.0868893	0.0780265
B. state/action	0.5	0.6	0.7	0.8	0.9	1.0
0.5	6.25626e-05	0.0125626	0.0250626	0.0375626	0.0500626	0.0625626
0.6	6.25626e-05	0.0500626	0.0250626	0.0375626	0.0500626	0.0625626
0.7	0.0001001 0.	0876001	0.1001	0.0376001	0.0501001	0.0626001
0.8	0.000175175	0.0876752	0.175175	0.150175	0.0501752	0.0626752
0.9	0.000262763	0.0877628	0.175263	0.262763	0.200263	0.0627628
1.0	0.00035035	0.0878503	0.17535	0.26285	0.35035	0.25035

Table 10. After 9999902 rounds for both pricebots. Simultaneous update with wA=0.25 and wB=0.75. 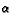$\alpha$is decaying starting at 0.001 rather than decaying at 0.01 as before. Note that 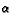$\alpha$is not fixed. $\epsilon$ has decayed to 0.0909092 using the regular $\epsilon$ decay at this point. Pricebots choose a random action for a state with probability of $\epsilon$ and choose the best action with probability 1-$\epsilon$ A. 1st qpricebot's table. Is in state 0.8 and action 0.7 on this round. The old Q value - the new Q value is 5.87092e-07. B. 2nd qlpricebot's table. Is in state 0.7 and action 0.7 on this round. The old Q value - the new Q value is 0.