Shoshana Neuburger
sneuburg@its.brooklyn.cuny.edu
CRA DMP Experience
Summer 2003

Homepage
Author
Journal
Research
Progress Report

Originally, random numbers were generated either manually or mechanically, by using such techniques as spinning wheels, dice rolling, or card shuffling. The modern approach is to use a computer to successively generate pseudorandom numbers. These pseudorandom numbers constitute a sequence of values, which although they are deterministically generated, all have the appearance of being independent uniform (0,1) random variables.

Computer games, medical trials, and stock market simulation all rely on the generation of random numbers. These sequences of numbers are all products of some algorithm; hence, each sequence of numbers can be predicted. These sequences of pseudorandom numbers must be tested extensively to determine whether they mimic the properties of truly pseudorandom needed in the simulation.

We all notice patterns in the numbers we must remember, such as telephone numbers and licenses. Therefore, the human mind alone cannot be trusted to judge whether a sequence of numbers is sufficiently random. Some unbiased mechanical tests must be applied to determine the usefulness of a particular random number generator. The theory of statistics provides us with some quantitative measures for randomness. Various tests compare whether a sequence is truly uniform and uncorrelated, truly a pseudorandom sequence.

This summer I am performing statistical tests on the shuffled nested weyl generator. For every test, the actual values are compared with those that would theoretically exist in a truly random number sequence. Often, software-graphing tools are used to simplify this comparison. When a significant deviation is found, it is important to document these discrepancies to warn all current and future users of the shuffled nested weyl generator to be aware of these deviations in their simulations.

One of the first tasks I faced in this project was that of coding the basic statistical tests that are reused in many tests. Since the shuffled nested weyl generator passed basic distribution tests before its first publication, I used the equidistribution test, since it is fairly simple to program, to validate the accuracy of my chi-square test and KS test.

The equidistribution Test determines that a sequence of numbers is evenly distributed over the interval (0,1). By sorting a fairly large number of samples into bins, and counting the number of observations that fall into each category, we demonstrated that the numbers were distributed evenly over each interval.

The chi-square test is a basic method that compares the expected behavior to the observed behavior with respect to a hypothesis. Performing the chi-square test on the results of the equidistribution test demonstrated that the distribution is within the expected range. Sorting many chi-square distributions and plotting the values based on their frequency revealed that the numbers are satisfactorily random with respect to this test. Figure 1 shows the plot of 1,000 chi-square distributions, each performed on 10,000 sorted samples.

The Kolmogorov-Smironov (KS) test is based on the difference between the theoretical and actual values of the cumulative probability distribution function for the test it is applied to, at different points. We applied the KS test to the equidistribution Test results. A fairly large number of KS calculations were obtained and the KS test was applied again to these results. This method of using several tests for moderately large numbers of samples, then combining the observations later in another KS test, tends to detect both local and global nonrandom behavior.

The shuffled nested weyl generator is often used for parallel, or distributed, calculations. It is important to verify that there are few correlations between parallel sequences. I tested pairs and triplets of numbers coming from two, three, four, five and six sequences, whether these sequences are taken in batches or in alternation. Figure 2 presents the variations in the distribution of the correlations (measured by comparing proximity of triplets) between two parallel sequences. Obviously, the sequences were taken from a slightly deviant variation of the shuffled nested weyl generator, in respect to its parallel-computing capabilities. The bell curve is still noticeable in the shape of the graph. These s equences passed all tests. However, when I tested seven parallel sequences taken in batches, I was startled to find large deviations from the expected results. I have developed a similar, yet different set of tests to test ten or more parallel sequences for correlations.

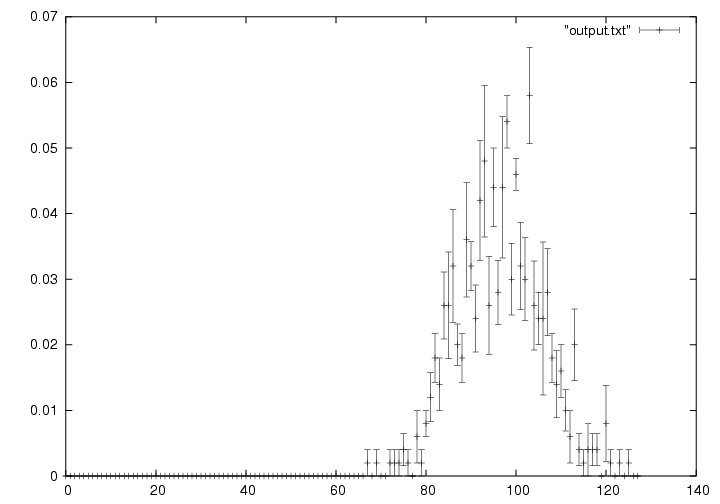
The nested weyl generator is known to fail in parallel-computing and distributed calculations. To demonstrate that my parallel test functioned properly, I ran the same test on several nested weyl pseudorandom sequences of numbers. As I expected, the nested weyl sequences deviated enormously from the ideal result of this parallel-computing test.

I used the minimum distance test to check that the minimum distance between the points generated correlates to the distance one would expect to find in a robust pseudorandom number generator. The shuffled nested weyl generator passed this test well.

Finally, I coded a test that finds the period of a random number generator by looking for a repetition of the first number in the sequence. If a match of the first number is found, a comparison of the next numbers is performed. This is repeated until a non-matching pair is found. I ran the code on a generator that had an obvious period of repetition and my program found the point of repetition. When I ran this test on the shuffled nested weyl generator, the program did not find any significant matches in the sequences of numbers provided by the shuffled nested weyl generator.

I hope to publish a paper in conjunction with Dr. Whitlock documenting our findings in our research of the shuffled nested weyl generator. In this capacity, we can advise the users of this random number generator as to how they can achieve the most accurate results in their simulations.