Originally, random numbers were generated either manually or mechanically, by using such techniques as spinning wheels, dice rolling, or card shuffling. The modern approach is to use a computer to successively generate pseudorandom numbers. These pseudorandom numbers constitute a sequence of values, which although they are deterministically generated, all have the appearance of being independent uniform (0,1) random variables.

Computer games, medical trials, and stock market simulation all rely on the generation of random numbers. These sequences of numbers are all products of some algorithm; hence, each sequence of numbers can be predicted. These sequences of pseudorandom numbers must be tested extensively to determine whether they mimic the properties of truly pseudorandom needed in the simulation.

We all notice patterns in the numbers we must remember, such as telephone numbers and licenses. Therefore, the human mind alone cannot be trusted to judge whether a sequence of numbers is sufficiently random. Some unbiased mechanical tests must be applied to determine the usefulness of a particular random number generator. The theory of statistics provides us with some quantitative measures for randomness. Various tests compare whether a sequence is truly uniform and uncorrelated, truly a pseudorandom sequence.

This summer I am performing statistical tests on the shuffled nested weyl generator. For every test, the actual values are compared with those that would theoretically exist in a truly random number sequence. Often, software-graphing tools are used to simplify this comparison. When a significant deviation is found, it is important to document these discrepancies to warn all current and future users of the shuffled nested weyl generator to be aware of these deviations in their simulations.

One of the first tasks I faced in this project was that of coding the basic statistical tests, that are reused in many tests. Since the shuffled nested weyl generator passed basic distribution tests before its first publication, I used equidistribution test, since it is fairly simple to program, to check the accuracy of my chi-square test and KS test.

The equidistribution Test determines that a sequence of numbers is evenly distributed over the interval (0,1). By sorting a fairly large number of samples into bins, and counting the number of observations that fall into each category, we demonstrated that the numbers were distributed evenly over each interval.

The chi-square test is a basic method that compares the expected behavior to the observed behavior with respect to a hypothesis. Performing the chi-square test on the results of the equidistribution test demonstrated that the distribution is within the expected range. Sorting many chi-square distributions and plotting the values based on their frequency revealed that the numbers are satisfactorily random with respect to this test. Figure 1 shows the plot of 1,000 chi-square distributions, each performed on 10,000 sorted samples.

The Kolmogorov-Smironov (KS) test is based on the difference between the theoretical and actual values of the cumulative probability distribution function for the test it is applied to, at different points. We applied the KS test to the equidistribution Test results. A fairly large number of KS calculations were obtained and the KS test was applied again to these results. This method of using several tests for moderately large numbers of samples, then combining the observations later in another KS test, tends to detect both local and global nonrandom behavior.

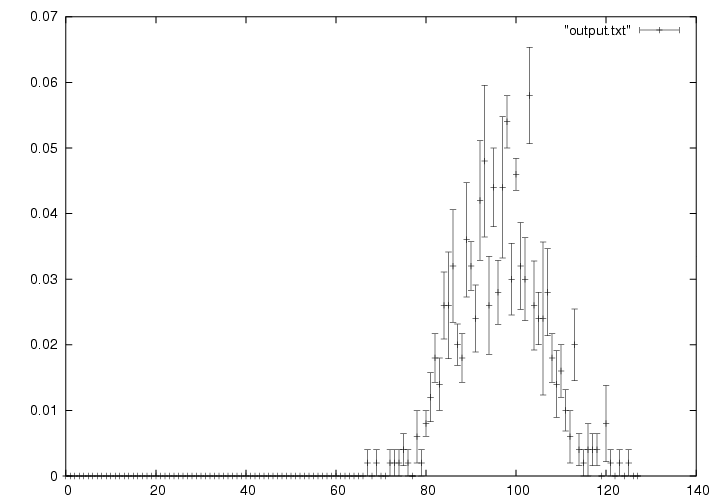
The shuffled nested weyl generator is often used for parallel, or distributed, calculations. It is important to verify that there are few correlations between parallel sequences. I tested pairs and triplets of numbers coming from two, three, four, five and six sequences, whether these sequences are taken in batches or in alternation. Figure 2 presents the variations in the distribution of the correlations (measured by comparing proximity of triplets) between two parallel sequences. Obviously, the sequences were taken from a slightly deviant variation of the shuffled nested weyl generator, in respect to its parallel-computing capabilities. The bell curve is still noticeable in the shape of the graph. These s equences passed all tests. However, when I tested seven parallel sequences taken in batches, I was startled to find large deviations from the expected results. I have developed a similar, yet different, set of tests to test ten or more parallel sequences for correlations.

My undergraduate research experience was greatly enhanced by my acquaintance with other undergraduate computer science students doing research in the college of my mentor. The weekly meetings with other faculty members and students helped familiarize myself with the research topics and methods employed by other students.

I am grateful that I have the opportunity to partake in this significant research experience without leaving my hometown. As a result, I am able to cherish the research experience without contending with boarding or the hassle of traveling this summer.

Over the next few weeks, I hope to conduct further parallel tests on the shuffled nested weyl generator. For example, does the minimum distance between pairs of numbers in the parallel sequences correspont to the expected average minimum distance? Also, I would like to test ten or mores sequences for correlations in three or more sequences.

At the end of my research project, I hope to document my findings and advise the users of this random number generator as to how they can achieve the most accurate results in their simulations.

Each of these tests' results should be within a specific range of values. This facilitates error catching and the correction of incorrect coding. This was also the source of my greatest frustration this summer. If the dividend of an equation is incorrect, there is nothing I can do to decrease the numbers by a factor of one million!

I have now completed the first six weeks of my summer research project. I hope the next four weeks prove to be as successful and enjoyable as the preceding weeks have been.