This week, I made my first attempt of determining what project I wanted to work on. My initial idea was based off of a technique I had seen used in the training of an OpenAI robot hand that learned to turn a cube via reinforcement learning inside of virtual reality. One of the key insights into how to get a system like this to work, is that they used domain randomization. This means that many of the colors and positions and other physical properties of things within the simulation were randomized between trials.

This forced the AI mechanisms they were using to generalize over a range of values, which helped them to be more robust in the real world. I wanted to explore ideas to see if I could come up with a process that would create a domain randomizer for any domain. That is, instead of OpenAI researchers determining what properties should be changed and within what ranges, they should be able to feed my program video feeds of the real situation, and the program would be able to determine properties that should be changed and within what range in order to have the best overall simulator for training the hand controller.
This idea led me straight into researching adversarial attacks on neural networks. Why? Well, adversarial attacks are done by very slightly changing an input image in order to trick a neural network into picking a different answer. (This Quora answer gives a decent overview of this phenomena.) So, any neural network that could deal with adversarial attacks likely had some sort of internal model as to how the input could change in ways that should not affect the output. This is essentially all that domain randomization is; determining how to change the input in ways that should not affect the output.
I debated researching this further, but during my research on adversarial attacks, I was brought back to the area of AI interpretability. (I attempted some work with AI interpretability last year, trying to see if capsule networks used concepts similar to humans.) This year, I decided I really wanted to understand what it meant for AIs to be interpretable. This is especially important to me since I'm concentrating in both computer science and philosophy, so this is a question topic that comes up a fair amount.
One of the papers I read made a distinction that I think is very important: persuasive systems versus transparent systems. In a different paper I read about last year, a researcher created an AI that used one system to make actions, and a completely different system that came up with justifications for those actions based off of the justifications humans had used when taking those same actions. I think this type of action explanation is awful, because it's persuasive instead of transparent. That is, the computer is merely giving you an explanation that looks plausible based off of the explanations humans have given previously. How the computer decides to make decisions in this case is not the same method that humans use to make decisions. So giving an explanation that is unrelated to how the AI functions I think is an extremely dangerous method, and I wish the authors had been more clear about the possible downsides of using their proposal.
I ended the week thinking that my main research was likely going to be in trying to come up with a new method (or at least a better definition) for interpretability in artificial intelligence.
My goal for this week was to understand two things:
One of the best papers I was able to find was What Good is an Explanation? by Peter Lipton. It was fairly old (2001), but very helpful in terms of understanding different philosophical explanations of understanding. I ended up giving a small presentation to my research group about the different models he proposes. Overall, I think the paper is helpful, but I don't quite agree with it. His main method was using three particular facts about explanations in order to show that certain definitions of an explanation either do or don't allow those three facts to be true. As a general principle, I think this approach works alright, but I think the facts he picked were odd, and not completely representative of what an explanation is (to me, at least). The facts were:
He gives a case that I think will help to explain these three facts. In this case, there is a ripped up stuffed teddy bear on the floor. We'd like an explanation as to why there is a ripped up stuffed teddy bear on the floor. In this case, we know that there is a ripped up stuffed teddy bear on the floor, but we don't understand why it is there. Also, an explanation may be that our pet dog ripped it up. This explanation works, even though we may not understand why the dog ripped it up. That is, the explanation still does a good job of explaining, without needing further explanation. Finally, part of the reason why we might think that the dog ripped up the stuffed teddy bear is because there is a stuffed teddy bear on the floor. That is, part of the evidence that the dog ripped up the stuffed teddy bear is the fact that the teddy bear is ripped up.
While I think these facts are true of some explanations, I'm not sure if they're true for all explanations, and so I think it's difficult to find good theories based on these explanations.
After reading his introduction and main argument, I ended up thinking that all of the theories he mentioned were properties of a good explanation. I won't detail my thoughts here, but I don't think the one account he chose ("Causality") is necessarily all that an explanation is; I think that each of the accounts he mentions is a property of explanations, and the more of those properties an explanation satisfies, the more likely we are to consider it to be a good explanation.
Overall, this helped me a lot with understanding how different people might categorize and understand explanations and AI interpretability.
Throughout the week, I also developed and tested my own definitions of AI interpretability. The one that seemed to make the most sense, and was the most stable, was Predictability. That is, in order for an AI to be interpretable, it must be predictable.
The analogy that I came up with isn't the best, but it at least gets at the idea. If there's a house, and we have ways of running inspections on the house to determine if it's safe to be in or not, then the house is predictable. That is, if the house passes the inspection, we know that it's safe to go in the house. However, if there is no inspection process, or houses that have passed inspection break without warning, then the house is not predictable.
A similar thing goes for AI. If the AI gives us explanations (or we "inspect" it to determine explanations for its behavior), then those explanations should allow us to predict how the AI will behave. To the extent that the explanations don't allow us to make accurate predictions about AI, I don't believe the AI should be considered "interpretable" or "safe" to use in high-stakes scenarios.
For example, we have yet to find very good ways to make neural networks interpretable. Why? Because in order to determine how the network will respond to a particular input, we currently have to send the vector through the network. That is, the best way to predict how the network will react is to see how it actually reacts. From the research I've done, we haven't found a good way yet of generalizing how neural networks will respond in particular cases. They're unpredictable. Thus, instances of adversarial attacks on networks still surprise us; neural networks are still unsafe.
Last week, in the middle of doing my own philosophical research, I also took a short break to look at some videos from the OpenAI Robotics Symposium on robotics. One of the talks on self-supervised learning really caught my interest. In the talk, they discuss how they were able to use a time-contrastive network (TCN) in order to teach a robot how to pour liquid into a cup, just from having it watch videos of people pouring liquid into a cup. I was very interested in how they did this, so I read the paper and more of the author's work to understand it.
I was especially interested if TCNs could be used in style transfer. Style transfer is an area that intrigues me due to my interests mentioned above about domain randomization and robust understanding (leading to predictability/interpretability). The idea is that if a computer can create the same product but in a different style, it likely understands what the product is. Essentially, domain randomization is just changing the style of the environment, without affecting core aspects of the environment itself. So if TCNs could be used for style transfer, they could likely be useful in these other problems as well.
At this point, I realized that I would be very interested in seeing if I could take the time-contrastive network from the paper and apply it to music. Instead of watching multiple people pour liquid into cups from multiple angles, and learning to imitate them, it would instead listen to the same song played with multiple different instruments, and then learn to output MIDI music with new instruments. This is the main idea behind my project for the summer.
So, as my mentor recommended, the first thing to do was to see if I could get Google's TCN up and running. I tried installing the software both in an Ubuntu virtual machine and straight on my Mac, but they both failed. Running on the Ubuntu VM didn't work because I didn't have a GPU, and running on my Mac didn't work because my Mac doesn't support the AVX instructions that the newer versions of Tensorflow use. (I have an old 17'' Mac.) And that was as far as I got this week.
After trying both of my personal computer options, it was time to move on to MSI and see if I could get the Google TCN up and running on there. I had to fight my way through a few bugs and re-accumulate to the supercomputing environment. (I had done some work for a graduate student last year on MSI.) But, in the end, I was able to get the tests up and running and passing.
However, after spending some time looking at the codebase and realizing that it would take me weeks to modify it in a way that might potentially be able to help me, I decided to look into implementing the paper (or at least the main ideas behind it) on my own. (Their implementation made a pretty ubiquitous assumption that the data you were using was video data, and it was going to take a while to figure out all the places where switching to audio would break their code and program workflow.)
So, I spent some time looking at recent advances both in using the triplet loss function (which is what the TCN uses to train) and style transfer. Over this period, I learned a lot about how the triplet loss function works, and about how it's normally used for face recognition.
I also ran into some very interesting audio style transfer projects. The best one was Facebook's AI Research's (FAIR) Universal Music Translation Network (UMTN). This does almost exactly what I want to do with TCNs (and it does it very well), but it edits the audio files directly. This is cool, but not exactly what I want. I want the computer to be able to write music similar to how humans do, by manipulating the notes, rather than the audio frequencies themselves. Since the UMTN edits the audio directly, it also ends up sounding a lot less clear than a recording of an actual instrument being played. They also mention this issue in the paper itself, as the results of one of their experiments show that the audio quality is nowhere near as good as an actual instrument. Using a MIDI output would hopefully get around this issue.
Another interesting find was the Google Magenta project, which worked more on the side of instrument blending, music structure, and audio transcription. Their piano to MIDI software is actually the best MIDI converter I've seen available online for free. I also like that they're doing the machine learning locally on the computer, so that they don't have to host the service - it makes it more likely that they'll leave it up and running since their costs will be minimal. (However, it does create a performance gap for people with computers that aren't very fast. A high-end gaming computer takes a second to do what may take another computer multiple minutes.)
Part of the workflow of the complete self-supervised imitation process is that a reinforcement learning algorithm uses the encodings learned from the TCN as a signal to judge its own performance. In my case, the AI would need to have some way of outputting MIDI notes which could be played, turning it into audio. Then, this audio would be passed through the TCN in order to get an encoding. This encoding is then measured against the encoding of the song that the AI is trying to imitate. The more different the MIDI encoding is from the song's encoding, the lower the reward the reinforcement learning part of the AI receives.
So, I decided to build a system that would allow an AI to output a vector and convert it into MIDI. I wanted it to be similar to how humans play instruments, so I decided that I wanted each number in the vector to symbolize a note. The AI could press down on a note by giving that note a value of .5 or higher (up to 1). The higher the value, the harder the note is pressed. Then, after a note is pressed, a value of .5 or higher again will release the note. This seemed to be similar enough to how humans play piano. There's no sustain pedal in this model, but the AI still has to determine when to press notes and when to release them. Each vector represented one beat of the song. How fast a beat is can be changed to allow the AI to have more precision.
I was able to get this system up and working, but did not find a suitable dataset to test to see if I could get a reinforcement learning algorithm to actually use it. It was hard to find datasets where I could convert either MIDI or audio into "press-and-release"-type vectors. I'm sure if I spent more time studying the MIDI format, I could have figured out how to reverse engineer the data, since I already found a program that forward-engineered it. The closest I got was being able to take audio files from a MIREX dataset which had the melody pitch annotated, and convert that into MIDI, so that the MIDI file could play the piano to exactly match the pitch of the main melody of the song. This, in turn, could be converted into the "press and release"-type vectors, if need be. However, this obviously wasn't what I wanted, because it sounded very forced - the piano would jump from note to note every hundredth of a second, trying to match the singer's pitch. What I wanted was MIDI files that sound like what a human would come up with if asked to transcribe a song.
For example, here is what the original song sounds like:
And this is what the MIDI transcript sounds like:
Not ideal. However, it's a step in the right direction.
This week basically ended with me having a working program that could convert the MIREX files into vectors, and convert those vectors into MIDI files that could then be played.
This week, I made progress on four different fronts.
The first area I made progress in was talking with John Harwell to see if there were any projects I could help with with regards to his work, and he mentioned that doing some background research and writing may be helpful.
The second area I made progress in was on the Universal Music Translation Network. In this case, it was backwards progress - I tried to get Facebook's implementation of the network up and running, but it turns out they used a particular GPU (the NVIDIA Tesla v100) and you can only use their network if you have that particular GPU. Thus, I determined that trying to experiment with the UMTN this summer was not going to be possible.
After that setback with the UMTN, I determined that maybe I could build a TCN by myself in Keras. (This is eventually the route that I took.) At this point, I was mostly planning - determining that I would need to implement the triplet loss function that the TCN uses (since it's not inherently implemented in Keras) and that I might want to use MNIST as my first dataset for testing.
The fourth front that I made progress on was realizing that it's very difficult to get neural networks to follow logical and sequential patterns exactly. For example, I highly doubt that an LSTM given multiple pages of simple addition equations such as 1 + 2 = 3 and 999 + 1 = 1000 would generalize to higher amounts of digits, even though that's how math works. My reasoning is that neural networks are extremely probabilistic - usually they will only come up with the correct answer a certain percentage of the time. Furthermore, when we say "correct answer", we're usually just taking the most "confident" answer from the neural network; neural networks give many answers with certain probabilities. Thus, it seems very difficult to ensure that a neural network will be able to follow a logical task with certainty. So, I found some papers to read about getting neural networks to follow logical papers. (Note that during Week 8, a paper came out describing a neural network architecture that allowed it to solve the Rubick's Cube puzzle with 100% accuracy on all of the cubes they gave it, showing that complex logical tasks can indeed be solved with neural networks.)
This week I decided to focus on implementing the triplet loss function in Keras, and testing it by using the MNIST dataset. Since the triplet loss was originally used to recognize faces, I figured it could also be used to recognize written digits as well. Ensuring that it worked on this dataset would provide at least a checkpoint along the way towards getting neural networks to create covers of other songs using MIDI.
Implementing the triplet loss was harder than expected. I had hoped that Keras had a triplet loss function already implemented, but it did not. Furthermore, I needed to learn about the functional API, because in order to use the triplet loss, I needed to use the same encoder on the three different inputs in order for the network to train. Finally, I needed to implement the loss function using the shared encoder and ensure that it trained correctly.
During this week, I was able to get TensorFlow up and running on my Mac, despite it not being able to follow AVX instructions. I found out that I was able to use TensorFlow version 1.5 without having to install from source. (I was weary about installing from source because it seemed more complex, and also if I received errors, it would be difficult for other people to verify whether it was the code or my installation that was the problem.) I then started to work on the triplet loss function, but was not able to get it working.
This week, I finally got the triplet loss function up and running. It took a few workarounds, and I also encountered an error that could not be reproduced with the new version of TensorFlow on a different computer. But eventually, I was able to get Keras to accept my triplet loss function and train.
One of the odd things about Keras is that it forces your loss function to be a function of two parameters: (inputs, outputs). But, with the triplet loss, we actually want our loss function to be a function of three parameters: (encoding of anchor image, encoding of positive image, encoding of negative image). Keras also checks to make sure that the dimensions of what you're passing to the loss function match up. This means that in order to trick Keras into using the triplet loss, I had to set the inputs to be a tensor with three dimensions on the first axis, one for each encoding. I then pass it a tensor containing the anchor, positive, and negative encodings within that shape. The outputs tensor is set to have the same shape in order to trick Keras. However, the the value we pass it is merely filled with zeros and contains no encodings since it will never be used. When customizing the loss function, we merely ignore the outputs parameter. This allows us to use the triplet loss in Keras.
Throughout the week, I also developed some functions useful for displaying results. For example, we can follow the network through a training session. In this session, I used a (deep) feedforward neural network with an inner layer of 200 neurons and an output layer of 100 neurons. I trained it on 100,000 randomly chosen triplets from the MNIST training set. I tested the model on 10,000 randomly chosen triplets from the MNIST test set. (It had never seen images from the test set before being evaluated on them.) We can follow how the network did on one of the triplets in the training set. In this case, the image of the number 1 in the top left is the anchor, the image of the number 1 in the top right is the positive example, and the image at the bottom of the number 5 is the negative example.
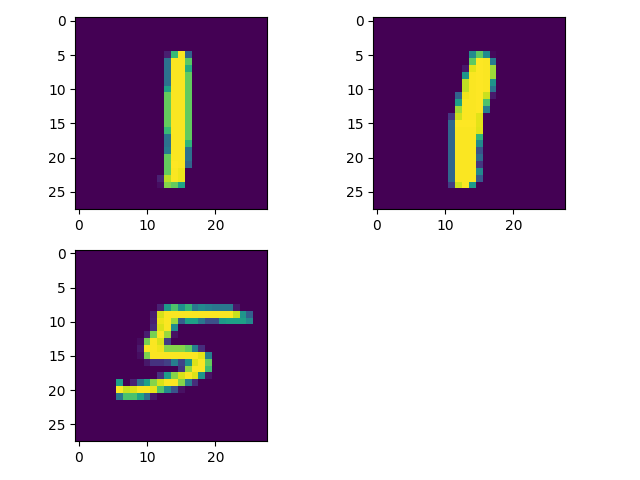
The goal of the network is to encode the images such that the encodings of the anchor and the positive example are as similar as possible, and the encodings of the anchor and the negative example are as different as possible. (It's just slightly more complicated than this, but that works as a simple explanation.) When the network hasn't done any training, the encodings look like this:
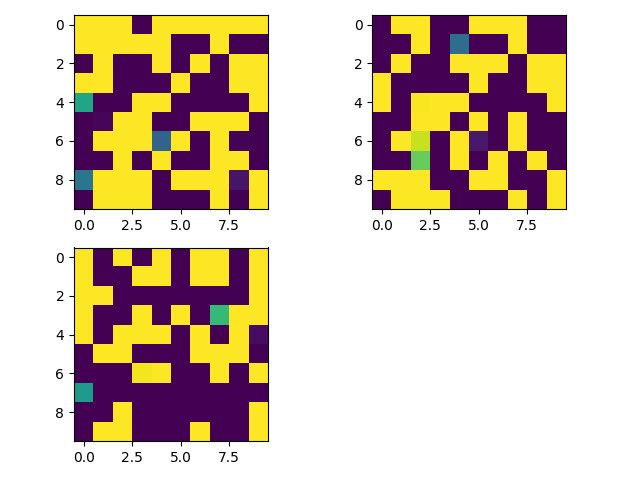
You can see that all three encodings look fairly different. We then train for 40 epochs, meaning that the network trains on all of the triplets 40 times in a row. (For those who want more technical details, I used a margin of .6 for the triplet loss, and the Adam optimizer with a learning rate of 0.0001 and batch size of 32.) I was able to graph both the triplet loss function and the accuracy. The triplet loss graphed is the average triplet loss over that epoch. The accuracy is defined as the percentage of triplets in the test set such that the encoding of the positive example is more similar to the encoding of the anchor than to the encoding of the negative example. (This is equivalent to determining the percentage of triplets in the test set with zero error, given a margin of 0 for the loss function.) Here are the graphs:
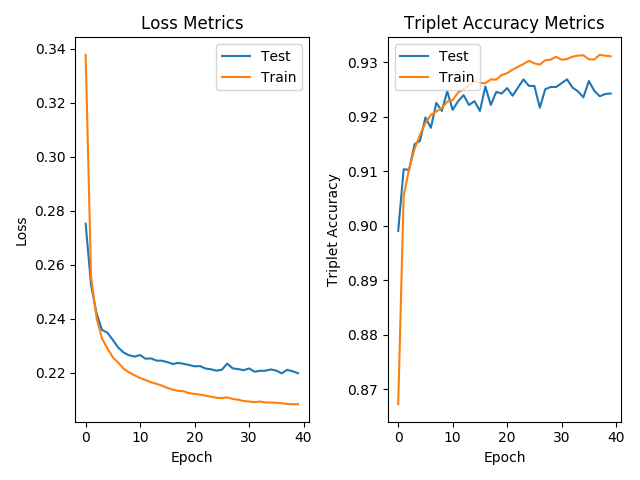
So, as we can see, it seems to train decently well, achieving over 92% accuracy, with the loss steadily decreasing and accuracy increasing over time.
We can then see what the final encodings look like after the 40 epochs:
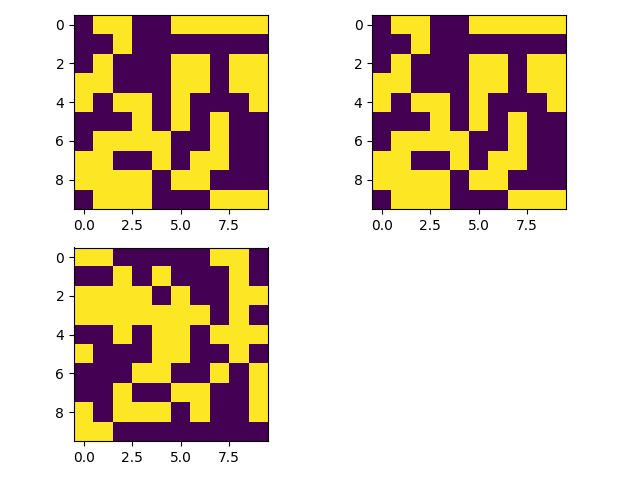
Notice that it worked! The encodings of the images of the number 1 are exactly the same, and the image of the number 5 has a very different encoding from those two.
With some progress made on my personal project, I focused more on working with John Harwell on his paper about the use of matroids in swarm robotics. I talked with him about his framework and how his method works, and started diving into the details of matroids and how to use them to prove that his method approximates a theoretically optimal method. We went through at least two drafts of a proof this week, and continued to work on the proof afterwards.
I also did some work this week trying to find a song cover dataset to train the TCN network on. I came across multiple different options, but in the end, most of them appeared to only have metadata about the songs due to copyright restrictions. I finally found a dataset put together for training for the MIREX competition, which is small (80 songs), but I believe may be big enough to work, given that songs consist of many "frames" of audio.
In addition, I started thinking about how to convert the triplet loss for the TCN into something that would work for song covers. Song covers are quite different from the videos used of people pouring liquids into cups, because they don't perfectly align. A cover of a song might hold a note for far longer than the original or use a different rhythm than the original song. Thus, the intuition I came up with this week is that the encodings for a song and a cover of that song should trace the same path through space. If you graph the encoding as a point in multidimensional space, and then connect the dots, the path should look the same between the song and its cover. However, there were two problems with this: 1. My intuition needed to be mathematically formalized. 2. The mathematical formalization may not have a derivative, which would make the network unable to train using this error function, because it wouldn't know how to minimize it.
This week was mostly focused on working with John Harwell to help with his paper on the use of matroids in swarm robotics. I was able to come up with a proof that a variation on his method of determining what tasks a robot should complete leads to the robots choosing the task that will maximize how many tasks they believe they will be able complete. This page was extremely helpful for understanding matroids and proofs that greedy algorithms work on matroids.
I also worked a fair amount on this journal as well during this week. (I enjoy the fact that that statement is slightly meta.)
I made some progress on my error function for audio as well. I realized that I could parameterize the paths in space so that both paths took the same amount of "time", and that as the path travels through space, I can change the time so that more time is covered when the path travels through more space. This essentially makes it so that if you hold onto the same note for longer, you don't move forwards in the song. The encoding of that note will be the same, so the vector will remain in the same place, and so time won't move forwards. I did not come up with a mathematical representation of this during the week, but that is the next step, in order to determine if the function has a derivative.
This week I worked on the paper with John Harwell, cleaning up the notation and making the proof more rigorous.
I also started working on attempting to compute the derivative of the error function idea I had, but because I'm approximating the "curves" by drawing straight lines between each of the output vectors of the network, the derivative ended up being a piecewise function, with at least one piece for every encoded portion of a song. Unfortunately, I don't think gradient descent (which is what neural networks use) will work very smoothly on these sorts of piecewise gradients, so it looks like my idea will need some revision.
I also started writing my final report as well, which can be found here.