Information About My Research

    I made a version of the Motion Planning method Rapidly-exploring Randomized Tree (RRT) in parallel. My research combines RRT and parallel computing. Motion Planning can thought of as a way to get an object from point A to point B. RRT is a widely used method to get the path we want from Point A to Point B. In regards to parallelizing this method, certain motion planning problems can take hours or days to get a solution. Because of this, parallel computing is used to reduce this overall time. Parallel computing can potentially knock hours, even days off the amount of time a problem would normally take to solve. I created my parallel RRT method under the guidance of my graduate advisor Sam Jacobs and faculty advisor Nancy M Amato.

    Motion planning is not only an important component of robotics, but also bio-informatics. As these fields progress and problem sizes increase, faster approaches need to be created. Parallel computation can be used to significantly speed up the computation. This paper studies the effects of parallelizing the Rapidly-exploring Randomized Tree (RRT) method, one of the two types of state-of-the-art sampling-based algorithms for solving motion planning problems. RRT helps solve motion planning problems by creating a tree to locally explore in C-Space. One implementation of parallel RRT updates the global tree immediately, which has a large communication overhead. The strategy proposed in this paper allows the user to specify how much of the tree will be created locally before updating the global tree shared amongst the processes. This paper experiments with various values of this k-parameter that is used to control the granularity of the local growth.

Here is a visual representation of the k-parameter variable described above:

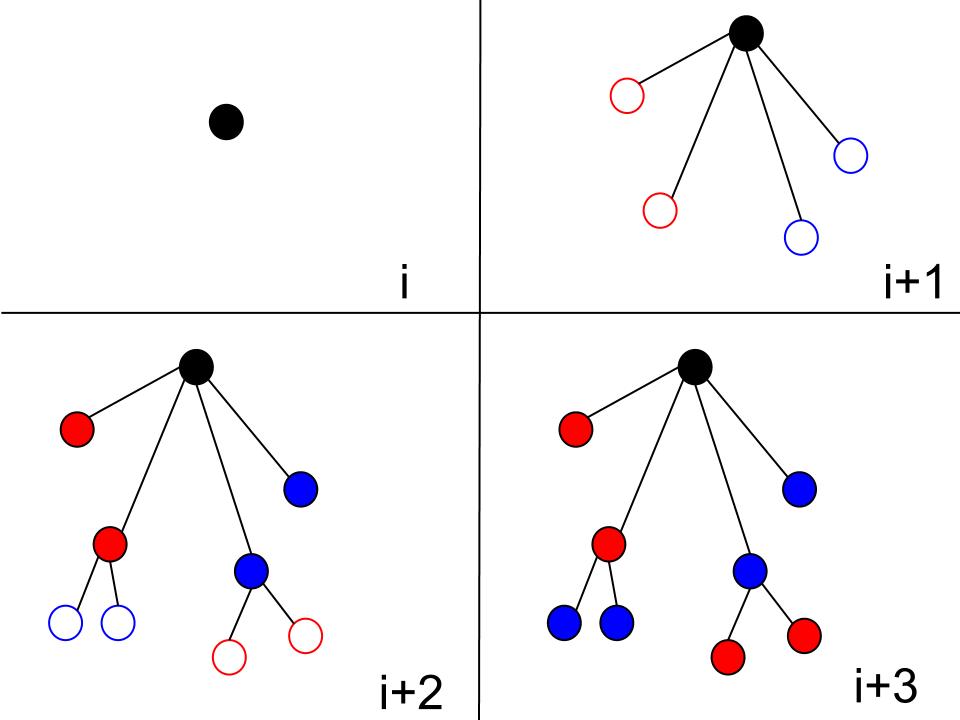
The black dot is the root of our overall tree. The red and blue colors represent two individual processors. My k-parameter equaled 2 in this example, so the overall tree grew by 4 nodes, two from both the red and blue processors, in sections i+1 and i+2. This process of a tre expanding by my k-paramter is the main point behind my research this summer. It is explained in a lot more detail in the paper, obviously.

Right-click the link and choose "Save Link As..." to save the document to your computer