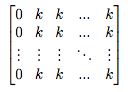This week went by well. The highlights from this week are as follows. On Monday, Lenore gave us (including  a few members of the ECE department) our first biology lecture. She gave an overview of the central dogma of biology (the process in which information from DNA is transcripted to RNA which is then translated into proteins) and went over other basic concepts. I also finished my program for arranging the DSD matrices. On Tuesday, I decided to look at the converged, arranged DSD matrices of graphs with five nodes to see if I could find any patterns. I looked at the three non-isomorphic trees and also began looking at the other eighteen matrices (corresponding to non-disjoint graphs on five vertices). I spent most of Wednesday doing this as well. I got a better picture of what my goal was: Can the arranged DSD matrix tell us anything about the topology of the network? Lenore gave me some guidance and told me to start looking at paths vs. complete graphs.  On Wednesday evening, Lenore invited us for a board game night at her house. This was a great way for all of us to bond and get to known one another outside the workplace. We had another group meeting on Thursday. This time, there was our group of six students, Donna's group of three, as well as Dr. Anselm Blumer and his two students. Each of us went around and introduced ourselves along with a brief description of what we were working on. After the meeting, I began to look at the converged, arranged DSD matrices for trees, complete graphs, and cycles for 3, 4, 5, and 6 - noded graphs. I noticed a pattern for complete graphs, so came up with a hypothesis and predicted what the matrix would look like for 7, 8, 9, and 10-noded graphs. These were validated by the program. The claim is as follows: